KECD 2195
Advanced topics in microeconometrics: Matching Models and their Applications
Sciences Po, Economics Department, PhD Course Spring 2018
Course information
Instructor: Alfred Galichon.
Schedule: Mondays, 8am-10am, starting January 29, 2016.
Class meets: Jan 29, Feb 5,12,19, Mar 5(+),12,19(+),26, Apr 9,16,23,30.
Location: 28 SP, H103.
Course material: Available on this github repository.
Texts
The first part of the course will be based on my (optional) text:
[OTME] A. Galichon (2016). Optimal Transport Methods in Economics, Princeton University Press.
Other textbooks used for reference (although not required) are:
[TSM] A. Roth and M. Sotomayor. Two-Sided Matching A study in Game-Theoretic Modeling and Analysis, Monographs of the Econometrics Society, 1990.
[DCMS] K. Train. Discrete Choice Methods with Simulation. 2nd Edition. Cambridge University Press, 2009.
[TOT] C. Villani, Topics in Optimal transportation, AMS, 2003.
Course material
Available after each lecture on the class webpage at url http://alfredgalichon.com/microeconometrics2018s.
Description of the Course
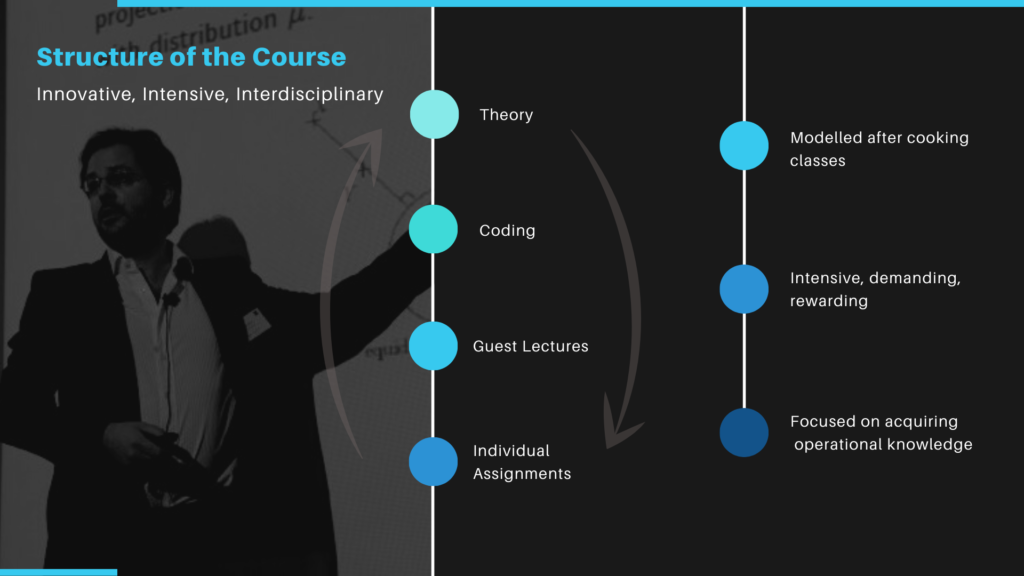
This course provides the mathematical and computational tools needed for an operational knowledge of discrete choice models, matching models, and network flow models. A number of economic applications of these concepts will be discussed.
The first part of the course will introduce basic results around Optimal Transportation theory: the Monge-Kantorovich duality, the Optimal Assignment Problem, basic results in Linear Programming, and Convex Analysis. Those concepts will serve as building blocks in the sequel.
The second part will cover discrete choice models, from the classical theory to more recent advances. The classical Generalized Extreme Value (GEV) specification will be recalled, as well as Maximum Likelihood estimation in the parametric case. Comparative statics results will be derived using tools from Convex Analysis, and nonparametric identification will be worked out using Optimal Transport theory. Simulation methods will be covered. A computationally intensive application will be demonstrated.
The third part will be devoted to matching models with stochastic utility, starting with the Transferable Utility (TU) case which is then generalized to Imperfectly Transferable Utility (ITU) including Non-transferable Utility (NTU). Equilibrium computation in the general case will be worked out using techniques from General Equilibrium. The more specific, but empirically relevant logit case, will be efficiently addressed using more the specific techniques or Iterative Fitting. Various algorithms will be described and compared in practice. Moment Matching Estimation and Maximum Likelihood Estimation will be worked out and compared. Several applications, to Collective Models of Family Economics, and to Labor Markets with taxes, will be described.
Time permitting, the fourth and last part will provide an introduction to problems on networks. The basic tools to describe the topology on a network will be described: discrete differential operators, diffusions on networks, shortest paths on networks. The Optimal Transport problem on networks will be formulated, along with its extension to stochastic utility.
Textbooks
The first part of the course will be based on my textbook:
• [OTME] Optimal Transport Methods in Economics (Princeton University Press, in press), a draft of which is available at http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2699381.
Other textbooks used for reference (although not required) are:
• [TSM] A. Roth and M. Sotomayor, Two-Sided Matching A study in Game-Theoretic Modeling and Analysis, Monographs of the Econometrics Society, 1990.
• [DCMS] Train, K.. Discrete Choice Methods with Simulation. 2nd Edition. Cambridge University Press, 2009.
• [TOT] C. Villani, Topics in Optimal transportation, AMS, 2003.
Organization of the Course
Part I: An introduction to Optimal Transport theory
L1. Monge-Kantorovich duality
• Primal and dual formulations
• The Monge-Kantorovich theorem
• Equilibrium and Optimality
Reference: [OTME] chapters 1 and 2.
Complements: [TOT], chapter 1.
L2. The optimal assignment problem
• Linear programming duality
• Purity, Stability
• Computation
Reference: [OTME], ch. 3, [TSM], Ch 8.
Complements: Shapley & Shubik (1972).
L3. The Becker model
• Copulas and comonotonicity
• Positive Assortative Matching
• The Wage Equation
Reference: [OTME], ch. 4. [TOT], Ch. 2.2
L4. Convex conjugacy
• Basics of convex analysis: Convex conjugates, Subdifferential, Fenchel-Young inequality
• Brenier’s theorem
Reference: [OTME], ch. 6. [TOT], ch. 2.1.
Part II: Discrete Choice models
L5. The logit model and its extensions
• The Logit model and its parametric estimation
• The Generalized Extreme Value (GEV) model
• The Daly-Zachary-Williams theorem
Reference: [DCMS], ch. 2-4, Anderson, de Palma & Thisse, Ch. 3, Carlier (2010).
L6. Identification of discrete choice models
• Reformulation as an Optimal Transport problem
• Consequences on the structure of the identifed set
• The Random Scalar Coefficient Model
• Incorporating peer effects
Reference: Hotz and Miller (1993), Chiong et al. (2014), Galichon and Salanie (2015).
L7. Simulation methods
• Simulation methods for parametric estimation
• Probit and the GHK simulator
• Simulation methods for nonparametric estimation
Reference: [DCMS], ch. 5 and 9, Chiong et al. (2014).
Part III: Matching models
L8. Models with transferable utility
• The TU-logit model of Choo and Siow
• Beyond Logit: general heterogeneity
• Simulation methods
• Moment matching estimation; Maximum Likelihood Estimation
Reference: Choo and Siow (2006), Galichon and Salanie (2015).
L9. Estimation of complementarity
• Index models
• Affinity matrix estimation
• Application: marital preference estimation
Reference: Chiappori, Oreffice and Quintana-Domeque (2012), Dupuy and Galichon (2014).
L10. Models with imperfectly transferable utility
• Equilibrium: Existence and Uniqueness
• The ITU-logit model
• Computation
• Maximum Likelihood Estimation
Reference: Galichon, Kominers and Weber (2015).
L11. Models with non-transferable utility
• Models with no idiosyncratic utility shocks
• Models with idiosyncratic utility shocks
Reference: Dagsvik (2000), Menzel (2015), Galichon and Hsieh (2015).
Part IV: Network models
L12. Optimal flow problems
• Basic concepts
• Min-cost flow problem
• Incorporating Stochastic Utility
Reference: [OTME], ch. 8. Koopmans (1949).
L13. Equilibrium flow problems
• Traffic equilibrium with congestion
• The Equilibrium Flow Problem.
Reference: Carlier (2010).
L14. Hedonic models
• Hedonic Equilibrium: definition and existence
• Estimation
Chiappori, McCann & Nesheim (2010), Ekeland, Heckman & Nesheim (2004), Dupuy, Galichon & Henry (2014).
Bibliography
• Anderson, de Palma, and Thisse (1992). Discrete Choice Theory of Product Differentiation. MIT Press.
• Aurenhammer, F. (1987). “Power diagrams: properties, algorithms and applications,” SIAM Journal on Computing.
• Becker, G. (1973). “A theory of marriage, part I,” Journal of Political Economy.
• Carlier, G. (2010). Lecture notes on “Optimal Transportation and Economic Applications.”.
• Chiong, K, Galichon, A., Shum, M. “Duality in dynamic discrete choice models.” Quantitative Economics, forthcoming.
• Choo, E., and Siow, A. (2006). “Who Marries Whom and Why,” Journal of Political Economy.
• Chiappori, P.-A., McCann, R., and Nesheim, L. (2010). “Hedonic price equilibria, stable matching, and optimal transport: equivalence, topology, and uniqueness,” Economic Theory.
• Pierre-André Chiappori, Sonia Oreffice and Climent Quintana-Domeque, C. (2012). “Fatter Attraction: Anthropometric and Socioeconomic Matching on the Marriage Market,” Journal of Political Economy 120, No. 4, pp. 659-695.
• Dagsvik, J. (2000) “Aggregation in matching markets,” International Economic Review 41, 27-57.
• Dupuy, A., and Galichon, A. (2014). “Personality traits and the marriage market,” Journal of Political Economy.
• Dupuy, A., Galichon, A. and Henry, M. (2014). “Entropy Methods for Identifying Hedonic Models,” Mathematics and Financial Economics.
• Ekeland, I., J. Heckman, and L. Nesheim (2004): “Identification and estimation of hedonic models,” Journal of Political Economy.
• Galichon, A. (2016). Optimal Transport Methods for Economics. Princeton University Press, in press.
• Galichon, A., Hsieh, Y.-W. (2015). “Love and Chance: Equilibrium and Identification in a Large NTU matching markets with stochastic choice”.
• Galichon, A., Kominers, S., and Weber, S. (2015). Costly Concessions: An Empirical Framework for Matching with Imperfectly Transferable Utility.
• Galichon, A., and Salanié, B. (2014). “Cupid’s Invisible Hand: Social Surplus and Identification in Matching Models”. Working paper.
• Heckman, J., R. Matzkin, and L. Nesheim (2010). “Nonparametric identification and estimation of nonadditive hedonic models,” Econometrica.
• Hotz, V.J. and Miller, R.A. (1993). “Conditional Choice Probabilities and the Estimation of Dynamic Models”. Review of Economic Studies 60, No. 3 , pp. 497-529.
• Koopmans, T. C. (1949), “Optimum utilization of the transportation system”. Econometrica.
• Menzel, K. (2015). Large Matching Markets as Two-Sided Demand Systems. Econometrica 83 (3), pages 897–941.
• Roth, A., and Sotomayor, M. (1990). Two-Sided Matching A study in Game-Theoretic Modeling and Analysis.
• Shapley, L. and Shubik, M. (1972) “The assignment game I: the core”. International Journal of Game Theory.
• Train, K. (2009). Discrete Choice Methods with Simulation. Cambridge University Press.
• Villani, C. (2003). Topics in Optimal transportation. Lecture Notes in Mathematics, AMS.
• Vohra, R. (2011). Mechanism Design. A Linear Programming Approach. Cambridge University Press.